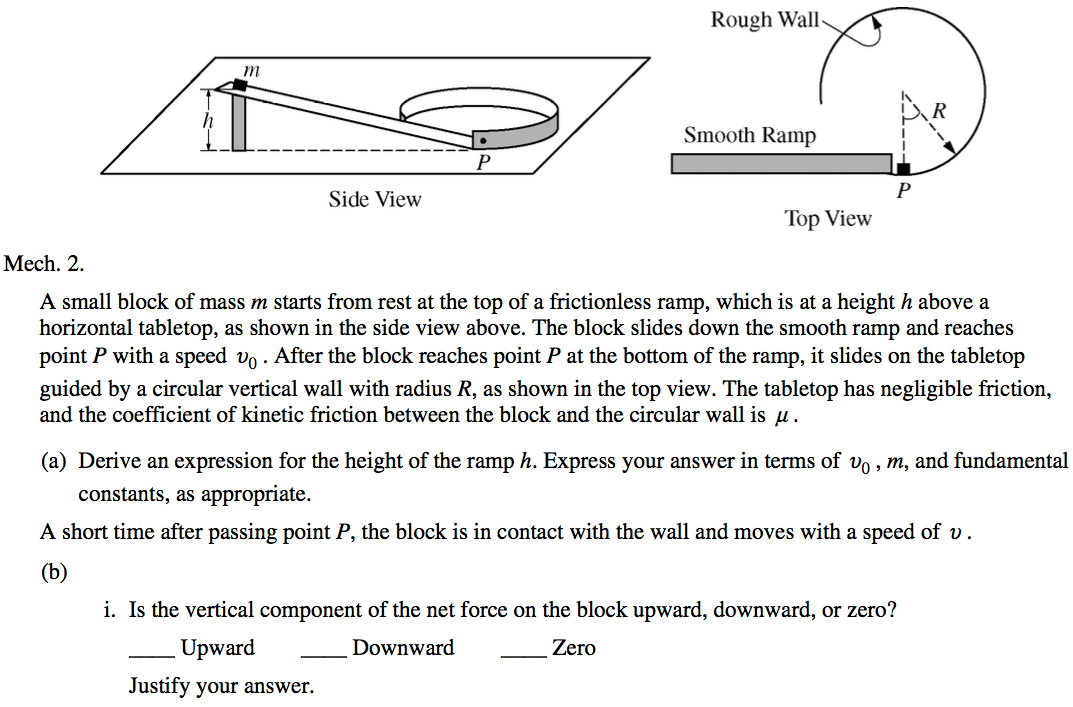
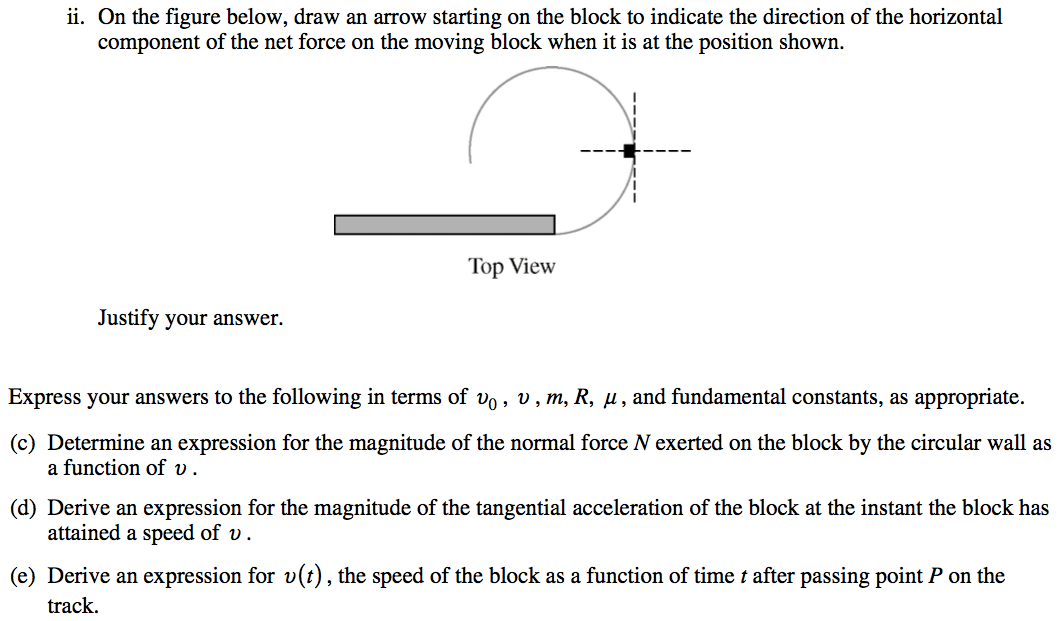
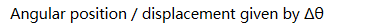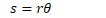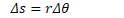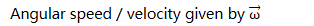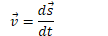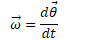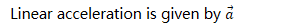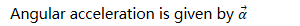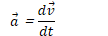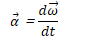Radians and Degrees

  • In degrees, once around a circle is 360°

  • In radians, once around a circle is 2π

  • A radian measures a distance around an arc equal to the length of the arc's radius

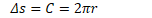
  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image174.png

Linear vs. Angular Displacement

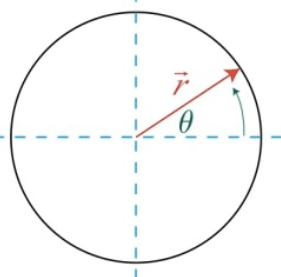
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image027.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image028.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image029.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image175.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image176.png

Linear vs. Angular Velocity

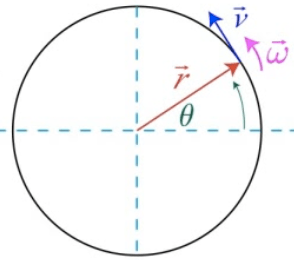
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image032.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image177.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image178.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image179.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image180.png

Direction of Angular Velocity

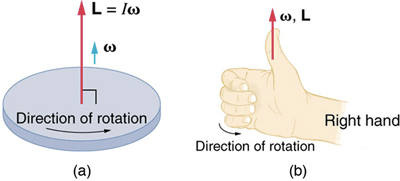
L = 10) irection of rotati Right hand Direction of rotation

Converting Linear to Angular Velocity

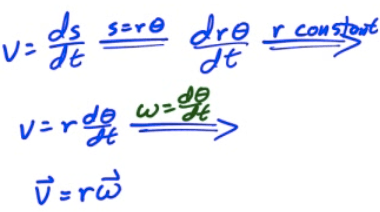
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image038.png

Linear vs. Angular Acceleration

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image039.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image181.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image182.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image183.png

  • C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image184.png

Kinematic Variable Parallels

Variable Translational Angular
Displacement Δs Δθ
Velocity v ⍵
Acceleration a ⍺
Time t t

Variable Translations

Variable Translational Angular
Displacement <img src="./media/image185.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image185.png"/ <img src="./media/image186.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image186.png"/
Velocity <img src="./media/image187.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image187.png"/ <img src="./media/image188.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image188.png"/
Acceleration <img src="./media/image189.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image189.png"/ <img src="./media/image190.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image190.png"/
Time <img src="./media/image191.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image191.png"/ <img src="./media/image192.png" alt="C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image192.png"/

Kinematic Equation Parallels

Rotational Motion (a = constant) 0=00 -Fat = — (00 + e = + —at2 02 = + 2a9 Linear Motion (a = constant) v vo + at vot + —at 2 2 = v: + 2ax

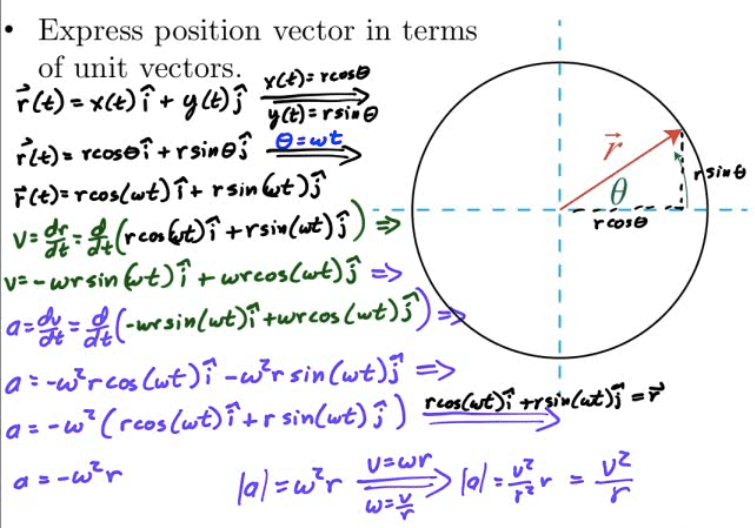
Centripetal Acceleration

Express position vector in terms of unit vectors. Fte)z r$in a —Jr sin

Example: Wheel in Motion

  • A wheel of radius r and mass M undergoes a constant angular acceleration of magnitude ⍺.

  • What is the speed of the wheel after it has completed on complete turn, assuming it started from rest?

    p_Uh

2003 Free Response Question 3

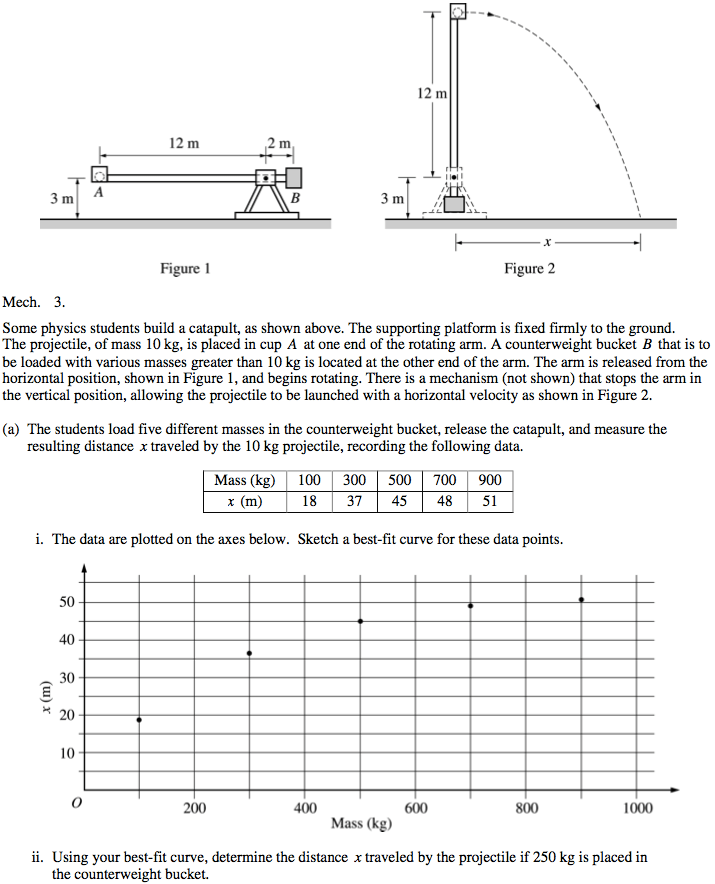
12 m Figure 1 Mech. 3. 12 m Figure 2 Some physics students build a catapult, as shown above. 'Ihe supporting platform is fixed firmly to the ground. •lhe projectile, of mass 10 kg, is placed in cup A at one end of the rotating arm. A counterweight bucket B that is to be loaded with various masses greater than 10 kg is located at the other end of the arm. The arm is released from the horizontal position, shown in Figure 1, and begins rotating. There is a mechanism (not shown) that stops the arm in the vertical position, allowing the projectile to be launched with a horizontal velocity as shown in Figure 2. (a) The students load five different masses in the counterweight bucket, release the catapult, and measure the resulting distance x traveled by the 10 kg projectile, recording the following data. Mass (kg) 100 300 500 700 18 37 45 48 900 51 i. The data are plotted on the axes below. Sketch a best-fit curve for these data points. 50 40 30 20 10 1000 Mass (kg) ii. Using your best-fit curve, determine the distance x traveled by the projectile if 250 kg is placed in the counterweight bucket.

(b) The students assume that the mass of the rotating arm, the cup, and the counterweight bucket can be neglected. With this assumption, they develop a theoretical model for x as a function of the counterweight mass using the relationship x = vxt, where v x is the horizontal velocity of the projectile as it leaves the cup and t is the time after launch. i. How many seconds after leaving the cup will the projectile strike the ground? ii. Derive the equation that describes the gravitational potential energy of the system relative to the ground when in the position shown in Figure 1, assuming the mass in the counterweight bucket is M. iii. Derive the equation for the velocity of the projectile as it leaves the cup, as shown in Figure 2. (c) i. Complete the theoretical model by writing the relationship for x as a function of the counterweight mass using the results from (b)i and (b)iii. ii. Compare the experimental and theoretical values of x for a counterweight bucket mass of 300 kg. Offer a reason for any difference.

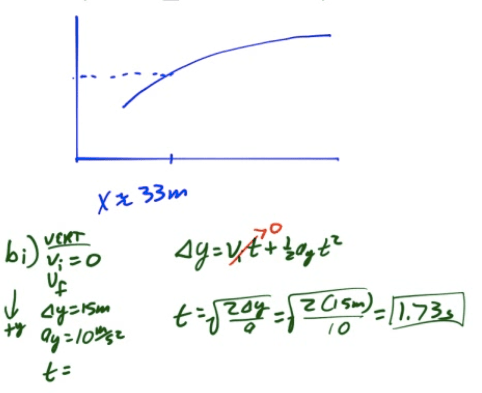
C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image196.png

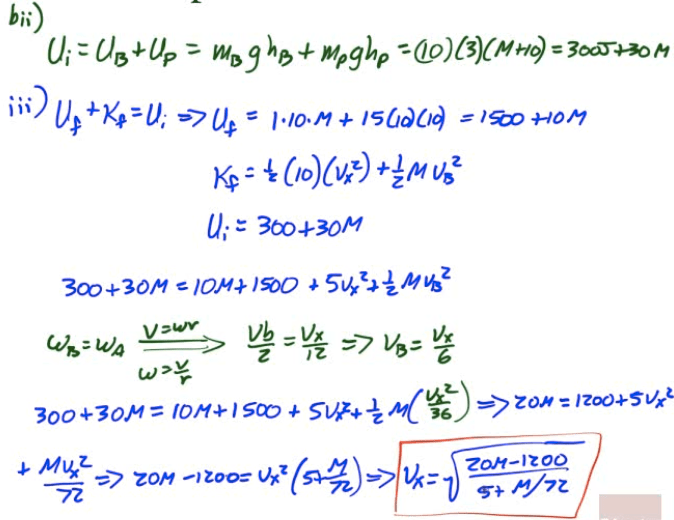
2Z/Q ,IS+OOZI MOZ + I *HO/ NOÉ* OOÉ t HQ€+CbÉ h.'OÉ+OQÉ zen + "•01•1 d'(6dH + q dntqn

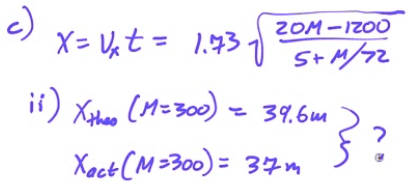
~ 0 一 00 37.

2014 Free Response Question 2

Rough Wall Smooth Ramp Side View Top View Mech. 2. A small block of mass m starts from rest at the top of a frictionless ramp, which is at a height h above a horizontal tabletop, as shown in the side view above. The block slides down the smooth ramp and reaches point P with a speed vo . After the block reaches point P at the bottom of the ramp, it slides on the tabletop guided by a circular vertical wall with radius R, as shown in the top view. The tabletop has negligible friction, and the coefficient of kinetic friction between the block and the circular wall is g . (a) Derive an expression for the height of the ramp h. Express your answer in terms of vo , m, and fundamental constants, as appropriate. A short time after passing point P, the block is in contact with the wall and moves with a speed of v . (b) i. Is the vertical component of the net force on the block upward, downward, or zero? Upward Justify your answer. Downward Zero

ii. On the figure below, draw an arrow starting on the block to indicate the direction of the horizontal component of the net force on the moving block when it is at the position shown. Top View Justify your answer. Express your answers to the following in terms of vo , v , m, R, g , and fundamental constants, as appropriate. (c) Determine an expression for the magnitude of the normal force N exerted on the block by the circular wall as a function of v . (d) Derive an expression for the magnitude of the tangential acceleration of the block at the instant the block has attained a speed of v . (e) Derive an expression for v(t) , the speed of the block as a function of time t after passing point P on the track.

C:\25225E85\B09A51C6-0574-4A0C-A2C1-496768C10C63_files\image201.png

= - ' = ッ 文 生 = プ み つ ン ↓ = イ 4 フ 台 = イ ウ - V 。 : + 女 些 : R + レ 善 レ イ ヨ →

results matching ""

    No results matching ""